Tutorial penyelesaian Markov Decision Process dengan pemrograman linier 🇮🇩
Published:
Pada postingan kali ini, kita membahas implementasi dari Markov decision process (MDP) sebagai alat untuk menyelesaikan permasalahan proses pengambilan keputusan dari sistem dinamik dengan memanfaatkan metode pemrograman linier. Pertama, kita akan membahas definisi dari MDP secara singkat. Lalu, kita akan melihat sebuah contoh kasus dari MDP untuk menentukan kebijakan optimal (optimal policy) dari perawatan mesin industri. Berdasarkan contoh kasus ini, kita akan membahas cara untuk menformulasikan representasi MDP yang sesuai. Terakhir, kita akan menyelesaikan representasi MDP tersebut dengan menggunakan teknik pemrograman linier untuk memperoleh keputusan optimal dari proses tersebut.
English version is available here.
Pengenalan Singkat
Markov decision process (MDP) adalah sebuah model matematis yang sering digunakan untuk memodelkan proses pengambilan keputusan stokastik dari sebuah proses dinamik. Dalam konteks ini, hasil dari sistem dipengaruhi oleh faktor random dan keputusan yang dibuat oleh agen, yang perlu membuat serangkaian keputusan berurutan dari waktu ke waktu. Komponen dasari dari MDP terdiri dari 4 tuples $(S, A, P_a, R_a)$, dimana:
- $S$ adalah set dari keadaan(state), yang seringkali disebut dengan state space.
- $A$ adalah set aksi yang disebut dengan action space ($A_s$ adalah set dari aksi yang tersedia dari keadaan $s$).
- $P_a(s,s’) = P_a(s_{t+1} = s’|s_t=s, a_t=a)$ adalah peluang dari aksi $a$ dalam keadaan $s$ dan waktu $t$ untuk bertransisi ke keadaan $s’$.
- $R_a(s,s’)$ adalah nilai imbalan (reward) dari pengambilan aksi $a$ untuk bertransisi dari keadaan $s$ ke keadaan $s’$.
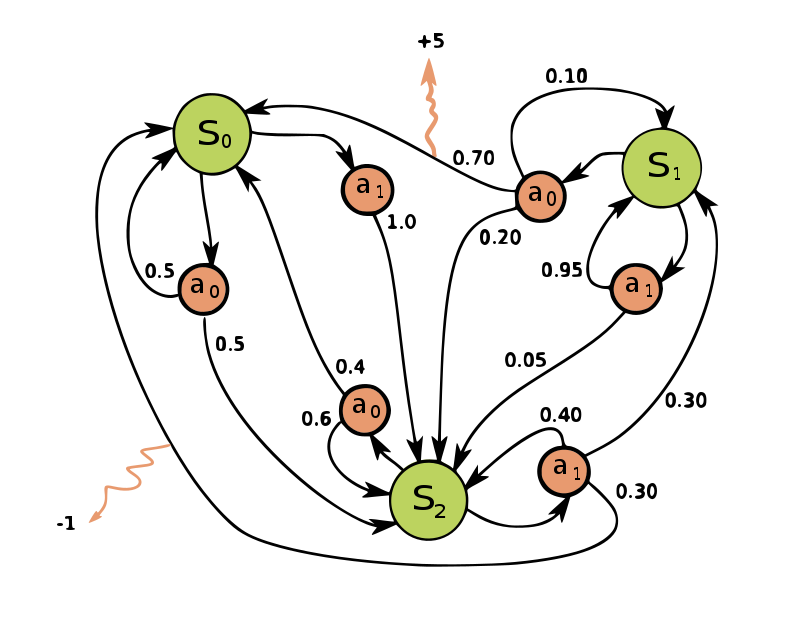
Gambar 1. Contoh sederhana dari MDP dengan tiga keadaan (lingkaran hijau), dua aksi (lingkaran oranye) dan dua *rewards* (panah oranye).
Seperti yang ditunjukkan dalam Gambar 1 [sumber], MDP sederhana tersebut memiliki tiga keadaan ($S_0, S_1, S_2$). Yang dimana, untuk tiap keadaan memiliki dua kemungkinan aksi ($a_0,a_1$) dan untuk tiap aksi yang diambil pada keadaan $s$ memiliki memiliki serangkaian probabilitas transisi unik yang mengarah ke keadaan $s’$ pada langkah waktu berikutnya. Dalam Gambar 1, nilai dari rewards hanya terdapat pada lokasi yang diindikasikan oleh panah oranye, sehingga kita dapat berasumsi bahwa proses lainnya memiliki nilai reward 0. Biasanya, representasi MDP seperti ini dapat diasumsikan untuk berjalan pada jumlah langkah waktu yang terbatas, seringkali disebut dengan MDP cakrawala terbatas (finite horizon MDP) (contoh: kampanye pemasaran yang berjalan selama 3 minggu). Atau, MDP tersebut juga dapat diasumsikan untuk berjalan tanpa batas waktu, seringkali disebut dengan MDP cakrawala tidak terbatas (infinite horizon MDP) (contoh: mesin yang berjalan 24/7 selama 10 tahun.)
Tujuan dari MDP adalah menemukan kebijakan optimal (optimal policy) yang mengatur pengambil keputusan, atau agen untuk membuat keputusan yang menghasilkan imbalan kumulatif terbesar dalam jangka waktu tertentu. Misalnya, kebijakan optimal pada Gambar 1 dapat berupa “Selalu lakukan $a_0$ dalam keadaan $S_0$, selalu lakukan $a_0$ dalam keadaan $S_1$, dan selalu lakukan $a_a$ dalam keadaan $S_2$” (disklaimer: Saya tidak tahu solusi optimal sesungguhnya, itu hanya contoh belaka).
Terdapat beberapa metode yang umum digunakan untuk memperoleh kebijakan optimum, seperti value iteration, policy iteration, dynamic programming, dll. Namun dalam tutorial ini kita akan membahas penyelesaian MDP menggunakan pemrograman linier, dan saya tidak akan membahas dasar teori terlalu banyak. Jika anda kurang familiar dengan konsepnya, saya merekomendasikan dua materi yang membahas dasar teorinya:
Agar lebih konkret, kita akan melihat contoh permasalahan MDP untuk menentukan kebijakan optimal dari proses perawatan mesin industri.
Rumusan Masalah
Sebuah mesin pasta tua beroperasi 7 hari selama seminggu dari jam 10.00 sampai jam 18.00. Karena mesin ini sangat penting bagi pabrik pasta, mesin tersebut perlu untuk dirawat secara rutin. Namun, karena mesin tersebut sudah cukup tua, mesin tersebut tidak memiliki sensor. Sehingga setiap paginya, teknisi pabrik perlu untuk memeriksa kondisi dari mesin dan mencatatnya. Menurut standar operasi pabrik, kondisi-kondisi mesin tersebut dapat dikategorikan menjadi 3: A (baik), B (biasa), C (jelek). Berdasarkan hasil inspeksi dari teknisi, manajer produksi membuat keputusan yang terdiri dari:
- Produksi normal $(N)$: Teknisi pabrik meninggalkan mesin dengan kondisi yang sekarang, mesin beroperasi secara normal.
- Perawatan dasar $(M)$: Teknisi melakukan perawatan dasar di pagi hari dengan biaya 3000 Euro. Perawatan dasar pada mesin dengan keadaan $B$ dapat mengubah kondisi mesin menjadi keadaan $A$ dengan peluang $0.2$ (selain itu tetap pada kondisi B), dan perawatan dasar pada mesin dengan keadaan $C$ dapat mengubah kondisi mesin menjadi keadaan $B$ dengan peluang $0.1$ (selain itu tetap pada kondisi C. Penting untuk dicatat bahwa setelah perawatan dasar di pagi hari, mesin tersebut tetap beroperasi secara normal.
- Overhaul $(O)$: Perawatan overhaul pada mesin akan selalu mengubah kondisi mesin menjadi keadaan A. Namun, perawatan overhaul memakan waktu sehari penuh dan mesin menjadi tidak produktif pada hari itu. Overhaul memakan biaya 4000 Eur.
Ketika mesin digunakan di dalam produksi, terdapat kemungkinan untuk kondisi mesin memburuk atau bahkan rusak. Peluang kejadian ini dipengaruhi oleh keadaan mesin saat itu. Kerusakan pada mesin dapat berakibat fatal, sehingga mesin membutuhkan 3 hari periode perbaikan (termasuk di hari ketika rusak), selama periode itu mesin tidak dapat digunakan untuk produksi. Pada hari keempat, mesin akan siap digunakan kembali dengan kondisi A. Secara rata-rata, kerusakan pada mesin menyebabkan kerugian total sebesar 23000 Euro, dengan menghitung seluruh biaya tenaga kerja, material, dan kerugian lainnya. Namun, jika mesin tersebut berhasil menyelesaikan satu hari produksi tanpa rusak, maka mesin tersebut dapat memproduksi pasta yang ekivalen dengan keuntungan sebesar 10000 Eur.
Berdasarkan data historis, insinyur kepala dari pabrik pasta tersebut telah menyajikan kita dengan informasi statistik yang berhubungan dengan kemungkinan mesin untuk memburuk dan rusak. Untuk merangkum semua informasi, data yang diberikan oleh insinyur kepala tersebut diberikan di Tabel 1. Namun, beberapa informasi belum diketahui dan kita perlu untuk menghitungnya.
Tabel 1. Informasi dari insinyur kepala.
| Keadaan | Aksi | Keadaan akhir | |||
|---|---|---|---|---|---|
| A | B | C | Rusak | ||
| A | Normal | 0.4 | 0.3 | 0.2 | 0.1 |
| B | Normal | - | ? | 0.4 | 0.3 |
| Maintenance | 0.2 | ? | ? | ? | |
| Overhaul | 1 | - | - | - | |
| C | Normal | - | - | ? | 0.4 |
| Maintenance | - | 0.1 | ? | ? | |
| Overhaul | 1 | - | - | - | |
Sebagai tambahan, informasi mengenai biaya dan keuntungan adalah sebagai berikut:
- Biaya perawatan dasar ($c_1$) = 3000 Eur
- Biaya overhaul ($c_2$) = 4000 Eur
- Total kerugian kerusakan ($c_3$) = 23000 Eur
- Keuntungan rata-rata harian ($d$) = 10000 Eur
Perumusan MDP
Formulasi yang akurat dari MDP merupakan hal yang krusial dalam representasi sistem dinamik. Terlebih lagi, dalam kasus ini kita masih memiliki informasi yang perlu untuk dihitung. Artikel ini tidak akan menjelaskan secara mendalam mengenai prosedur untuk mengkonstruksi representasi grafik MDP. Namun, dalam kasus ini akan diberikan hasil akhir dari representasi MDP kemudian akan dijelaskan alasan dibaliknya. Gambar 2 adalah hasil akhir dari representasi MDP untuk permasalahan yang diberikan.

Gambar 2. Representasi grafik MDP.
Pertama, dalam kasus ini kita dihadapi dengan permasalahan mesin yang beroperasi 7 hari dalam seminggu dengan ekspektasi penggunaan mesin untuk dalam jangka waktu yang panjang. Sehingga kasus ini dapat disederhanakan sebagai kasis MDP dengan cakrawala tidak terbatas (infinite horizon). Dalam kasus ini, kita memiliki keadaan utama dari MDP yaitu $(A,B,C,Br_1)$ yang direpresentasikan oleh bentuk persegi dan aksi utama yaitu operasi normal ($N$), perawatan dasar ($M$), dan overhaul ($O$). Dalam keadaan baik $A$, kita hanya perlu untuk mempertimbangkan aksi operasi normal ($N$) sebagai opsi untuk keadaan ini. Lalu, berdasarkan Tabel 1, kita dapat mengetahui peluang mesin untuk berganti keadaan dan kita dapat menggambarkan panah yang ke keadaan yang berkorespondensi dengan nilai peluang yang ditulis dalam teks berwarna hijau. Hal yang sama juga berlaku untuk keadaan $B$ dan $C$ ketika beroperasi dalam kondisi normal. Namun, dalam tabel satu, informasi $P(B|B,N)$ dan $P(C|C,N)$ masih tidak diketahui. Hal ini dapat dengan mudah diselesaikan dengan mengetahui bahwa jumlah dari peluang transisi untuk tiap aksi pada tiap keadaan harus sama dengan 1:
\[\sum_{s'\in S'} P(s'|s,a) = 1,\]sehingga kita mendapatkan $P(B|B,Normal) = 0.3$ dan $P(C|C,Normal) = 0.6$.
Keadaan menjadi sedikit lebih rumit ketika kita perlu untuk mempertimbangan aksi perawatan dasar. Sebagai contoh, perawatan dasar pada keadaan $B$, kita mengetahui bahwa perawatan dasar tersebut dapat memperbaiki keadaan mesin menjadi $A$ dengan peluang $P(A|B,M) = 0.2$. Namun, kita juga tahu bahwa mesin tersebut masih dapat beroperasi dengan normal setelah perawatan dasar, sehingga mesin tersebut masih memiliki kemungkinan untuk memburuk atau bahkan rusak. Sehingga peluang transisinya dapat dihitung dengan:
- $P(B|B,M) = (1 - P(A|B,M)) \cdot (P(B|B,N)) = 0.24$
- $P(C|B,M) = (1 - P(A|B,M)) \cdot (P(C|B,N)) = 0.32$
- $P(Br_1|B,M) = (1 - P(A|B,M)) \cdot (P(Br_1|B,N)) = 0.24$.
Dengan prosedur yang serupa, kita dapat menghitung probabilitas transisi untuk perawatan dari keadaan $C$, dengan hasil yang ditampilkan pada Gambar 2. Proses overhaul selalu mengubah kondisi mesin menjadi $A$ dan mesin tersebut tidak dapat beroperasi dengan normal pada hari tersebut, sehingga kita dapat merepresentasikan proses overhaul dengan satu entitas saja. Hal ini dikarenakan tidak ada perbedaan dalam probabiliitas transisi dan nilai imbalan (reward) untuk overhaul pada kondisi $B$ maupun $C$.
Memodelkan kerusakan pada mesin dapat sedikit rumit, dinyatakan bahwa:
Kerusakan pada mesin dapat berakibat fatal, sehingga mesin membutuhkan 3 hari periode perbaikan (termasuk di hari ketika rusak), selama periode itu mesin tidak dapat digunakan untuk produksi. Pada hari keempat, mesin akan siap digunakan kembali dengan kondisi A.
Sehingga, kita dapat mengasumsikan pada hari pertama (hari kerusakan) mesin tersebut masih dalam kondisi sebelumnya dan kita membutuhkan blok ekstra untuk memodelkan 2 hari ekstra dari periode perbaikan. Demi kelengkapan, kita representasikan tiap hari dengan pasangan keadaan dan aksi, hari kedia direpresentasikan dengan pasangan $(Br_1,R)$ dan hari ketiga direpresentasikan oleh $(Br_1,R)$, dimana probabilitas transisinya adalah $P(Br_2|Br_1,R) = 1$ and $P(A|Br_2,R) = 1$.
Lalu, kita dapat menghitung nilai ekspektasi imbalan / reward dari tiap aksi pada tiap keadaan dari mesin tersebut. Untuk mensimplifikasi, kita mulai dari yang paling mudah terlebih dahulu, yaitu kerusakan. Kita dapat mengasumsikan bahwa bagian ini memiliki imbalan 0 karena biaya kerugian akibat kerusakan telah dimasukkan kedalam biaya kerugian 23000 Euro, seperti yang dinyatakan dalam rumusan masalah, sehingga:
- $r(R|Br_1) = 0$
- $r(R|Br_2) = 0$
Selanjutnya, nilai dari imbalan untuk overhaul pada keadaan $B$ dan $C$ juga cukup sederhana. Dikarenakan mesin tidak dapat beroperasi pada hari itu, nilai dari imbalan untuk overhaul pada keadaan $B$ dan $C$ adalah -4000 Euro, tanda negatif menunjukkan bahwa pabrik pasta tersebut mengeluarkan uang.
- $r(O|B) = c_2 = -4000$
- $r(O|C) = c_2 = -4000$
Untuk kondisi operasi normal pada keadaan $A$, $B$, dan $C$, kita perlu mempertimbangkan bahwa tiap keadaan memiliki peluang untuk rusak, diberikan pada tabel 1, dengan rata-rata total kerugian -23000 Euro, dan keuntungan dari beroperasi secara normal sebesar 10000 Euro. Dikarenakan keuntungan dari operasi tidak bergantung pada keadaan dari mesin (kecuali rusak), perhitungan imbalannya menjadi relatif mudah:
- $r(N|A) = P(Br_1 | A,N) c_3 + (1-P(Br_1 | A,N))d = 6700$
- $r(N|B) = P(Br_1 | B,N) c_3 + (1-P(Br_1 | B,N))d = 100$
- $r(N|C) = P(Br_1 | C,N) c_3 + (1-P(Br_1 | C,N))d = -3200$
Terakhir, kita pertimbangkan kasus perawatan dasar untuk keadaan $B$ dan $C$. Prosedur perhitungan imbalan untuk skenario ini sama persis dengan perhitungan imbalan pada kondisi normal, namun dengan tambahan biaya perawatan dasar $c_1$. Sehingga proses perhitungannya menjadi:
- $r(M|B) = c_2 + P(Br_1 | B,M) c_3 + (1-P(Br_1 | B,M))d = -920$
- $r(M|C) = c_2 + P(Br_1 | C,M) c_3 + (1-P(Br_1 | C,M))d = -4880$
Sekarang, kita dapat menempatkan semua informasi di dalam MDP, dimana nilai dari imbalan dituliskan dalam teks merah. Secara sekilas dari hasil perhitungan tersebut, skenario perawatan dasar tidak memiliki keuntungan dikarenakan nilai dari imbalan menunjukkan bahwa pabrik tersebut akan cenderung untuk kehilangan uang daripada menghasilkan keuntungan. Namun, untuk detil dari kebijakan optimalnya, kita perlu untuk menyelesaikan representasi MDP dengan metode pemrograman linier yang akan dibahas pada bagian setelah ini.
Pemrograman linear untuk MDP
Sampai dengan tahap ini, anda dapat menyelesaikan MDP yang telah diformulasikan dengan metode seperti value iteration, policy iteration, dynamic programming, dll. Namun, dalam tutorial ini, kita akan menyelesaikan MDP dengan pemrograman linier.
Catatan: Dalam tutorial ini, saya menggunakan Gurobi karena saya memiliki lisensi akademik. Namun, anda juga dapat menggunakan library open source seperti CVXPY atau Pyomo. Interface dari library tersebut mungkin berbeda, namun ide umum cara penyelesaian tetap sama.
Tujuan utama dari penyelesaian MDP (menemukan kebijakan optimal) adalah memaksimalkan jumlah dari imbalan kumulatif dari waktu ke waktu. Secara matematis, ekspresi ini ditulis sebagai:
\[\max \sum_{s\in S}\sum_{a\in A} r(a|s)x_{a|s},\]dengan konstrain:
\[\sum_{s\in S}\sum_{a\in A} x_{a|s} = 1,\] \[\sum_{a\in A} x_{a|s} = \sum_{s'\in S}\sum_{a\in A} p(s|s',a)x_{a|s'} \quad \forall s \in S,\] \[x \geq 0\]dimana $x_{a|s}$ adalah probabilitas agen untuk memilih aksi $a$ di dalam keadaan $s$ pada periode random. Ekspresi $r(a|s)$ menyatakan imbalan dari melakukan aksi $a$ di dalam keadaan $s$, dan $p(s|s’,a)$ adalah probabilitas transisi untuk mencapai keadaan $s$ ketika agen di dalam keadaan $s’$ dan melakukan aksi $a$. Mungkin, penjelasan diatas agak sedikit membingungkan. Namun, kita akan bahas lebih detil dalam memformulasikan permasalahan di dalam kode.
Pertama-tama, kita impor library dalam Python dan inisiasi model pemrograman linier:
import numpy as np
import gurobipy as gp
lp = gp.Model()
Sekarang, definisikan variabel keputusan $x_{a|s}$ di dalam model. Penting untuk dicatat bahwa kita memiliki konstrain $x \geq 0$, dalam kasus ini kita aplikasikan langsung kedalam batasan nilai variabel.
# Adding variables to the model
# args `lb=0.0` means the lower bound of the variable is 0.0
x_AN = lp.addVar(name="x_AN", lb=0.0)
x_BN = lp.addVar(name="x_BN", lb=0.0)
x_BM = lp.addVar(name="x_BM", lb=0.0)
x_BO = lp.addVar(name="x_BO", lb=0.0)
x_CN = lp.addVar(name="x_CN", lb=0.0)
x_CM = lp.addVar(name="x_CM", lb=0.0)
x_CO = lp.addVar(name="x_CO", lb=0.0)
x_Br1R = lp.addVar(name="x_Br1R", lb=0.0)
x_Br2R = lp.addVar(name="x_Br2R", lb=0.0)
Untuk fungsi objektif dari MDP:
\[\max \sum_{s\in S}\sum_{a\in A} r(a|s)x_{a|s},\]karena komponen $r(a|s)$ telah ditentukan oleh informasi yang tersedia, kita hanya dapat mengontrol variabel $x_{a|s}$. Pada konteks fungsi objektif, hal ini dapat diterjemahkan secara kasar menjadi “Maksimalkan nilai imbalan total dengan memilih variabel keputusan $x_{a|s}$ yang tepat”. Sehingga, secara spesifik dalam kasus kita, fungsi objektifnya dapat ditulis sebagai:
\[\max r(N|A)x_{N|A} + r(N|B)x_{N|B} + r(M|B)x_{M|B} + r(O|B)x_{O|B} + r(N|C)x_{N|C} + r(M|C)x_{M|C} + r(O|C)x_{O|C}\]Agar singkat, kita dapat langsung memasukkan nilai dari tiap reward. Pada Python, ekspresi ini ditulis sebagai:
# Define the objective function
lp.setObjective(6700*x_AN + 100*x_BN - 920*x_BM - 4000*x_BO - 3200*x_CN - 4880*x_CM - 4000*x_CO, gp.GRB.MAXIMIZE)
Selanjutnya, kita memiliki konstrain pertama. Konstrain ini hanya memberi tahu bahwa jumlah probabilitas tindakan yang kita ambil dengan mempertimbangkan periode acak harus sama dengan satu. Pada titik ini, variabel keputusan $x_{a|s}$ mungkin tampak agak abstrak. Mengapa kita menganggap probabilitas mewakili keputusan yang harus kita ambil? Untuk saat ini, kita akan biarkan dan kembali lagi nanti dalam pembahasan hasil. \(\sum_{s\in S}\sum_{a\in A} x_{a|s} = 1,\)
Dalam kasus ini, dapat ditulis sebagai:
\[\sum x_{N|A} + x_{N|B} + x_{M|B} + x_{O|B} + x_{N|C} + x_{M|C} + x_{O|C} + x_{R|Br_1} + x_{R|Br_2} = 1\]Dalam Python:
# Add first constraint
c1 = lp.addConstr(x_AN + x_BN + x_BM + x_BO + x_CN + x_CM + x_CO + x_Br1R + x_Br2R == 1, "action prob")
Lalu, kita lihat konstrain kedua. Walaupun terlihat sedikit membingungkan, konstrain ini menyatakan bahwa untuk tiap keadaan, “jumlah” atau “besaran” dari panah yang masuk kedalam blok keadaan harus sama dengan “jumlah” atau “besaran” yang keluar. Sehingga secara matematis ditulis sebagai:
\[\sum_{a\in A} x_{a|s} = \sum_{s'\in S}\sum_{a\in A} p(s|s',a)x_{a|s'} \quad \forall s \in S,\]Untuk tiap blok keadaan:
- $x_{N|A} = p(A|A,N)x_{N|A} + p(A|B,M)x_{M|B} + p(A|B,O)x_{O|B} + p(A|C,O)x_{O|C} + p(A|Br_2,R)x_{R|Br_2}$
- $x_{N|B} + x_{M|B} + x_{O|B} = p(B|A,N)x_{N|A} + p(B|B,N)x_{N|B} + p(B|B,M)x_{M|B} + p(B|C,M)x_{M|C}$
- $x_{N|C} + x_{M|C} + x_{O|C} = p(C|A,N)x_{N|A} + p(C|B,N)x_{N|B} + p(C|B,M)x_{M|B} + p(C|C,M)x_{M|C} + p(C|C,N)x_{N|C}$
- $x_{R|Br_1} = p(Br_1|A,N)x_{N|A} + p(Br_1|B,N)x_{N|B} + p(Br_1|B,M)x_{M|B} + p(Br_1|C,M)x_{M|C} + p(Br_1|C,N)x_{N|C}$
- $x_{R|Br_2} = p(Br_2|Br_1,R)x_{R|Br_1}$
Dalam Python ditulis:
# Add second constraint
c2 = lp.addConstr(x_AN == 0.4*x_AN + 0.2*x_BM + x_BO + x_CO + x_Br2R, "state A constr")
c3 = lp.addConstr(x_BN + x_BM + x_BO == 0.3*x_AN + 0.3*x_BN + 0.24*x_BM + 0.1*x_CM, "state B constr")
c4 = lp.addConstr(x_CN + x_CM + x_CO == 0.2*x_AN + 0.4*x_BN + 0.32*x_BM + 0.6*x_CN + 0.54*x_CM, "state C constr")
c5 = lp.addConstr(x_Br1R == 0.1*x_AN + 0.3*x_BN + 0.24*x_BM + 0.4*x_CN + 0.36*x_CM, "state Br1 constr")
c6 = lp.addConstr(x_Br2R == x_Br1R, "state Br2 constr")
Terakhir, kita jalankan program:
lp.optimize()
Ketika menjalankan program, kita akan mendapatkan tampilan seperti yang ditunjukkan pada gambar 3:
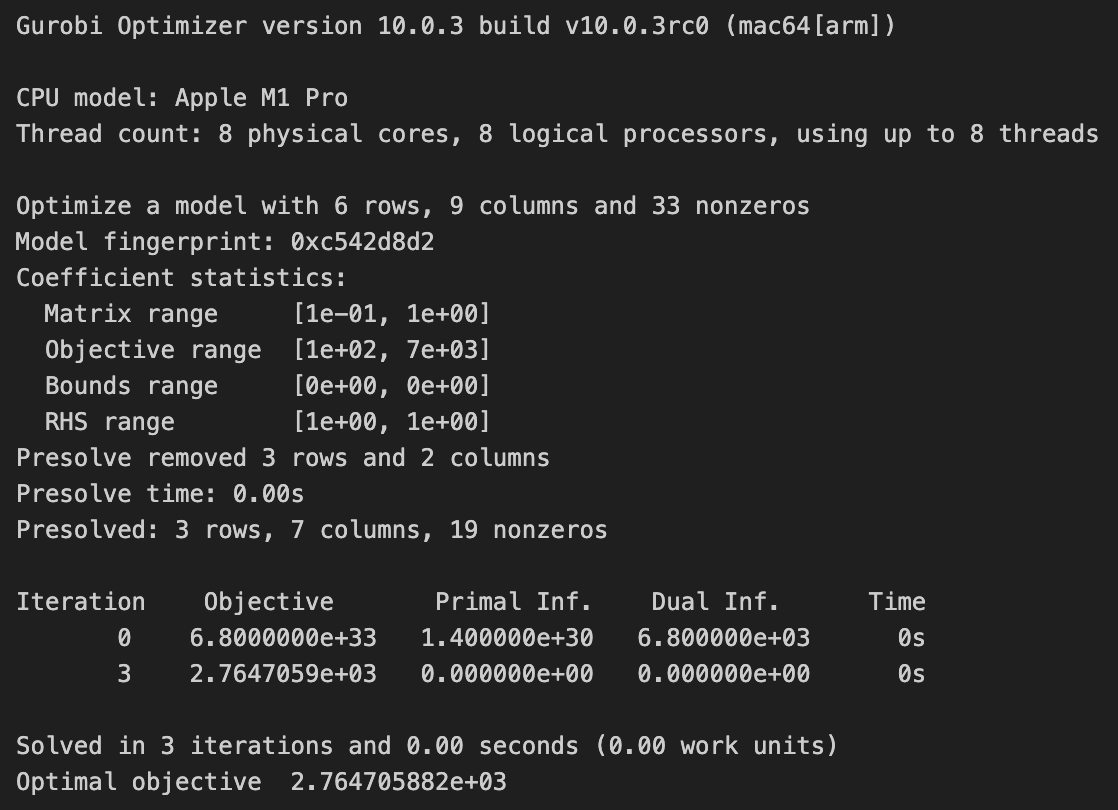
Gambar 3. Tampilan program.
Lalu kita ekstrak hasilnya:
{var.VarName : var.x for var in lp.getVars()}
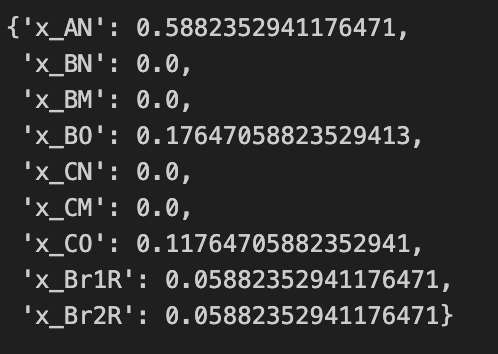
Gambar 4. Kebijakan optimal.
Hasilnya menunjukkan kebijakan optimalnya adalah:
| State | A | B | C | Br_1 | Br_2 |
|---|---|---|---|---|---|
| Action | Normal | Overhaul | Overhaul | Repair | Repair |
Dengan imbalan $\approx 2765$ Euro.
Sekarang, kita kembali untuk menginterpretasi nilai variabel keputusan. Kita lihat $x_{O|B} \approx 0.1765$ sebagai contoh. Dalam ekspresi ini, nilai probabilitas atau peluang dapat diterjemahkan sebagai nilai ekspektasi dari frekuensi kejadian. Sehingga, dapat diinterpretasikan sebagai “Jika kita mengikuti kebijakan optimal dan menjalankan MDP sebanyak 10000 langkah waktu (hari), maka kita dapat berekspektasi untuk menemukan mesin di keadaan $B$ dan membuat keputusan untuk overhaul kurang lebih sebanyak 1765 kali.”.
Sitasi artikel ini:
@misc{faza2024mdplptutorial,
author = {Faza, Ghifari Adam},
title = {Tutorial on solving Markov Decision Process with linear programming},
month = {May},
year = {2024},
url = {https://fazaghifari.github.io/posts/2024/05/mdp-lp-en/},
}
