Prediksi Bidang Vektor (Vector Field) Sederhana dengan Proper Orthogonal Decomposition dan Polynomial Chaos Expansion (POD-PCE) 🇮🇩
Published:
Dalam artikel ini, kita mengeksplorasi penggunaan proper orthogonal decomposition (POD) dan polynomial chaos expansion (PCE) sebagai surrogate model untuk memprediksi perilaku bidang vektor pada rentang waktu sembarang. Dibandingkan dengan metode surrogate model standar lainnya seperti regresi PCE standar atau regresi Gaussian process (GP) standar, penambahan komponen POD memiliki kelebihan untuk menganalisis data dalam bidang vektor dengan mentransformasi bidang vektor seperti aliran fluida pada video dibawah menjadi representasi yang lebih ringkas.
Artikel versi bahasa inggris dapat diakses disini
Proper orthogonal decomposition (POD), juga dikenal dengan dekomposisi Karhunen-Loéve [1] adalah metode analisis teknik untuk
memperoleh aproksimasi dari representasi dimensi rendah untuk aliran turbulen [2], analisis struktur [3], dan sistem dinamik [4]. Sederhananya, POD mentransformasi bidang vektor seperti aliran fluida pada video dibawah menjadi representasi yang lebih ringkas.
Video 1. Ilustrasi aliran fluida.
Sebagai orang awam, mungkin pada awalnya akan terasa cukup aneh. Mengapa kita butuh representasi yang lebih ringkas dari aliran fluida tersebut? Salah satu kasus yang umum adalah, representasi ringkasi dari aliran fluida tersebut dapat digunakan untuk memprediksi perilaku dari permasalahan tersebut jika diberikan parameter yang belum pernah terobservasi sebelumnya. Sebagai contoh, jika video di atas mendeskripsikan aliran fluida dari $t=0$ sampai $t=5$, kita dapat memprediksi bentuk alirannya saat $t=6$ dengan menggunakan representasi ringkas tadi.
Mengingat bahwa sebuah bidang vektor dapat terdiri dari beberapa sampai jutaan elemen. Memprediksi nilai tiap elemen pada bidang vektor tersebut bukanlah hal yang mudah. Sehingga, dengan POD, kita dapat menyederhanakan permasalahan tersebut dengan memprediksi representasi ringkasnya saja, alih-alih memprediksi tiap elemen.
Formulasi POD
Data Masukan
Input standar dari POD adalah matriks dengan ukuran $N \times m$ dimana $N$ adalah jumlah dari elemen di dalam bidang vektor, dan $m$ adalah jumlah dari variasi parameter. Dalam kasus ini, parameter yang digunakan adalah waktu $t$. Sehingga, anda juga dapat mengganti variabel $m$ dengan $t$ dalam contoh ini. Matriks $N \times m$ ini seringkali disebut dengan matriks snapshot. Skematik dari pembentukan matriks snapshot ditunjukkan dalam gambar 2:
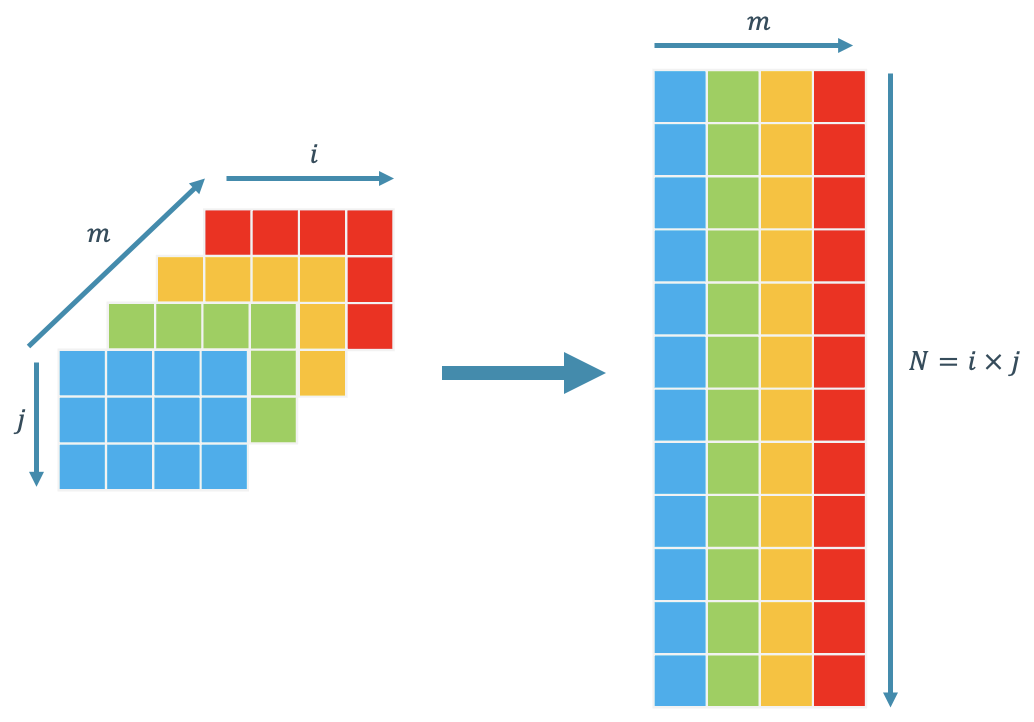
Gambar 2. Skematik pembentukan matriks *snapshot*.
Dalam kasus aliran fluida yang kita gunakan, data dari aliran fluida pada tiap langkah waktu perlu diratakan seperti yang terpampang pada gambar 3. Data yang telah diratakan kemudian disusun sedemikian rupa sehingga tiap kolom dari matriks snapshot merepresentasikan satu langkah waktu.
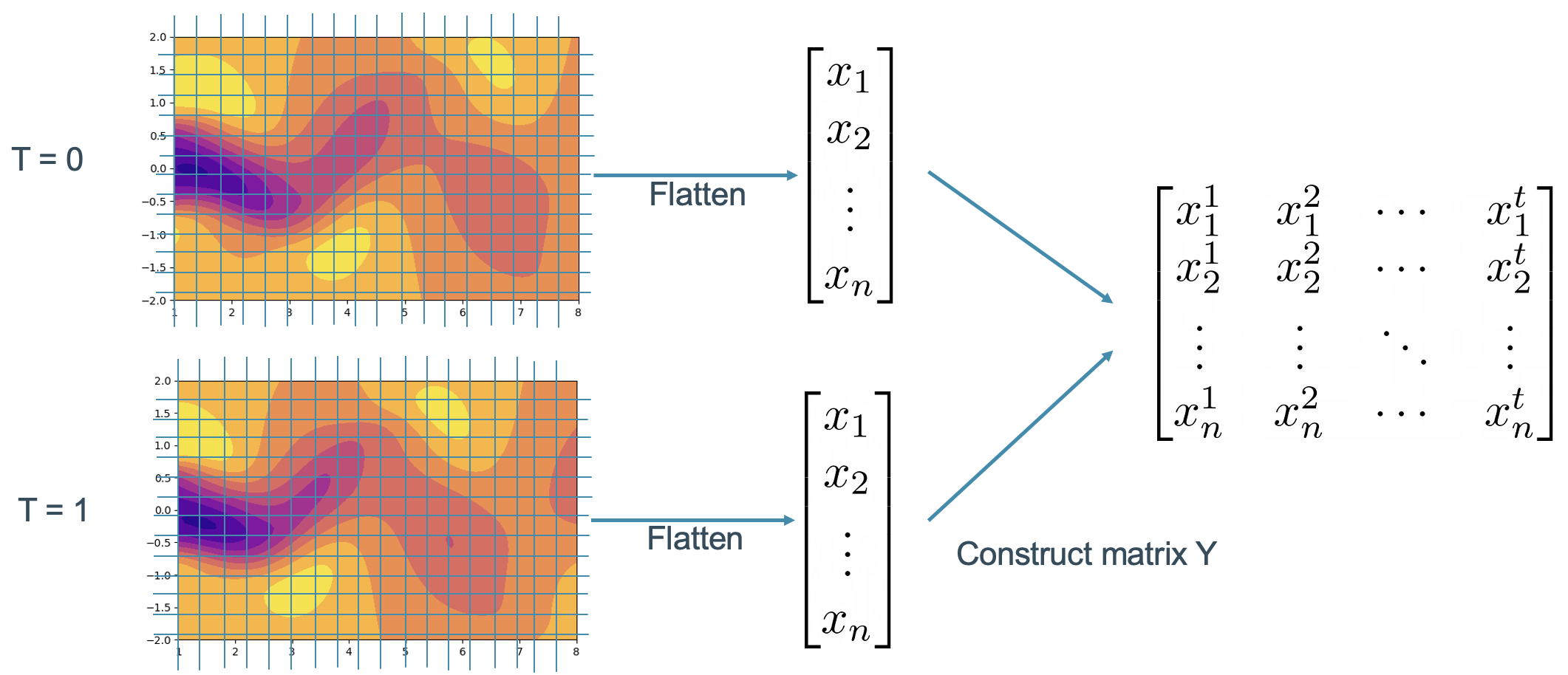
Gambar 3. Proses pembentukan matriks snapshot untuk kasus aliran fluida.
Agar lebih praktis, dalam artikel tutorial ini akan disertakan kode Python untuk melakukan analisis. Data yang digunakan dalam artikel ini dapat diunduh disini.
Data yang diberikan memiliki beberapa komponen diantaranya adalah U_star (komponen kecepatan arah $x$ dan $y$), p_star (komponen tekanan), t_star (waktu), and X_star (koordinat spasial). Pada artikel ini, kita akan fokus kepada kecepatan x sebagai variabel yang dianalisis dan koordinat spasial untuk membuat grafik. Pertama, kita ekstrak datanya:
import numpy as np
import scipy.io
import matplotlib.pyplot as plt
data = scipy.io.loadmat("cylinder_nektar_wake.mat")
u_star = data['U_star'] # N x 2 x T -- 2 indicates u_x (1st axis) and u_y (2nd axis)
p_star = data['p_star'] # N x T
t_star = data['t'] # T x 1
x_star = data['X_star'] # N x 2
Dalam kasus ini, semua variabel sudah tersedia dalam bentuk yang telah diratakan. Sehingga, kita tidak perlu meratakannya sendiri. Namun, penting untuk diketahui, untuk membuat grafik, kita perlu untuk membentuk kembali data koordinat spasial x_star kedalam bentuk $50 \times 100$. Untuk kasus ini, bentuk asli dari x_star adalah $N \times 2$, dimana kolom pertama adalah koordinat $x$ dan kolom kedua adalah koordinat $y$.
# Reshape Data
x_grid = x_star[:,0].reshape(50,100)
y_grid = x_star[:,1].reshape(50,100)
Seperti yang sudah dijelaskan, dalam kasus ini kita hanya fokus kepada komponen kecepatan x, sehingga kita hanya akan memilih komponen pertama dari sumbu kedua dari u_star u_star[:,0,:]. Dengan melakukan pilihan seperti ini, kita telah membuat matriks dengan ukuran $N \times T$, yang sesuai dengan ukuran matriks snapshot yang diinginkan.
snapshot = u_star[:,0,:]
Sampai tahap ini, kita telah selesai untuk membuat matriks snapshot. Namun, jika anda ingin membuat grafik dari satu langkah waktu dari matriks snapshot, anda dapat memilih satu kolom dari matriks snapshot, membentuk kolom yang sudah dipilih menjadi $50 \times 100$, dan menggambar grafik. Hasil gambar grafiknya akan terlihat mirip seperti gambar 4.
single_snapshot = snapshot[:,42] # Select one column (any column, here I choose column 42)
ux_grid = single_snapshot.reshape(50,100) # Reshape selected column to 50 x 100
# Simple Plotting
plt.contourf(x_grid,y_grid,ux_grid)
plt.xlabel('x')
plt.ylabel('y')
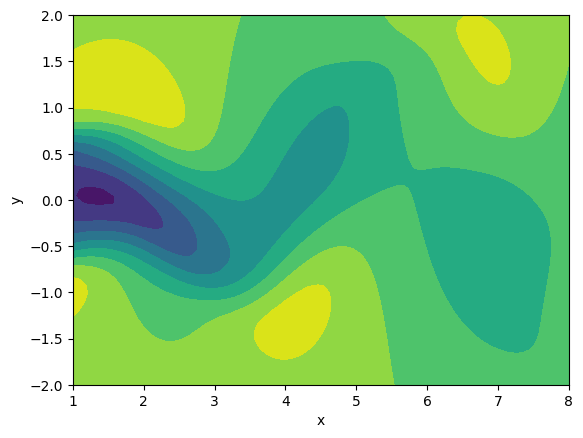
Gambar 4. Plot aliran fluida dalam satu waktu.
Matrix Decomposition
Algoritma dekomposisi nilai singular (SVD) [5] digunakan di dalam POD. Mungkin beberapa dari anda pernah atau telah mengetahui metode ini, namun, jika anda lupa, atau belum pernah belajar mengenai aljabar linear, saya akan menjelaskan kosep dari POD sesederhana mungkin.
Dengan SVD, jika kita memiliki matriks $Y$, matriks tersebut dapat didekomposisi menjadi komponen matriks $Y$ into $U$, $\Sigma$ (Detail dari dekomposisi matriks tidak akan dijelaskan secara detil di dalam artikel ini, karena kita dapat menggunakan modul dari Python seperti numpy. Namun, jika anda tertarik, saya pribadi merekomendasikan video ini oleh Prof. Gilbert Strang)
\[Y = U \Sigma_r V^T\]Pada konteks kasus yang sedang kita bahas, matriks $Y$ adalah matriks snapshot. Matriks $U$ dapat diinterpretasikan sebagai matriks yang merepresentasikan komponen spasial. Matriks $V$ adalah matriks yang merepresentasikan komponen parameter lain, dalam kasus ini, adalah komponen waktu. Matriks $\Sigma_r$ adlaah matriks diagonal dengan rank $r$ yang merepresentasikan “kekuatan” dari basis yang sesuai. Nilai diagonal dari matriks $\Sigma_r$ terdiri dari nilai singular $Y$ yang disusun secara menurun sehingga $\sigma_1 \geq \sigma_2 \geq \ldots \geq \sigma_r$. Nilai rank $r$ dari dekomposisi nilai tunggal (SVD) ditentukan dari nilai terkecil antara $N$ dan $m$. Secara matematis, pernyataan ini dapat ditulis sebagai $\min(N,m)$. Bentuk dari hasil akhir dekomposisi diilustrasikan dalam Gambar 5.

Gambar 5. Ilustrasi SVD.
Dalam Python, dekomposisi SVD dapat dilakukan dengan mudah. Dalam melakukan dekomposisi ini kita perlu menyatakan parameter full_matrices=False agar mendapatkan bentuk output yang diinginkan. Jika tidak, bentuk yang didapatkan tidak akan sesuai (dapat dibaca (disini)[https://numpy.org/doc/stable/reference/generated/numpy.linalg.svd.html]). Seperti yang dijelaskan di dalam dokumentasi tersebut, bentuk bawaan dari s adalah array dengan bentuk $r \times 1$. Sehingga, agar konsisten dengan definisi $\Sigma_r$ kita perlu mengubahnya menjadi matriks diagonal. Perlu diperhatikan juga bahwa hasil dari vt merupakan matriks $V$ yang terlah di-transpose.
u,s,vt = np.linalg.svd(snapshot,full_matrices=False)
sigma = np.diag(s)
Dengan mengasumsikan bahwa $r = \min(N,m)$, kita mendapatkan bahwa dimensi akhir dari matriks $U$ masih sama dengan matriks snapshot aslinya. Sehingga, jika kita hanya berhenti sampai sini, hasil dari dekomposisi tersebut masih tidak efisien secara memori komputasi. Kita dapat memotong $r$ dengan memilih sebuah angka $k$ yang dimana $k < r$. Untuk menentukan nilai $k$, pertama kita dapat menentukan secara bebas bergantung pada masukan pengguna. Atau kita dapat melakukan aproksimasi nilai $k$ dengan:
\[\begin{gathered} \frac{\sum^k_{i=1} \sigma_i}{\sum^r_{i=1} \sigma_i} \geq \alpha, \quad k\in \mathbb{Z}^+\\ r = \min(N,m), \end{gathered}\]dimana $\sigma_i$ adalah elemen diagonal dari $\Sigma$ yang disusun secara menurun sehingga $\sigma_1 \geq \sigma_2 \geq \ldots \geq \sigma_r$. Variabel $\alpha$ dapat diinterpretasikan sebagai besarnya “variasi” yang dapat dideskripsikan oleh model yang terpotong. Atau, menurut interpretasi bebas saya, variabel tersebut adalah tingkat “akurasi” yang ingin dijaga di dalam model yang terpotong. Biasanya, nilai yang dipilih adalah $\alpha = 0.99$. (Catatan: Kode untuk versi $k$ dengan input user tidak diberikan di dalam artikel ini dan diserahkan kepada pembaca sebagai latihan)
# Determine number k
temp = 0
alpha = 0.99
diagsum = np.sum(s)
for idx, sigma in enumerate(s):
temp += sigma
ratio = temp/diagsum
if ratio >= alpha:
k = idx
break
# truncate matrices
s_trunc = s[:k]
u_trunc = u[:,:k]
vt_trunc = vt[:k,:]
sigma_trunc = np.diag(s_trunc)
Sehingga, kita memiliki:
\[Y \approx U_k \Sigma_k V^T_k\]Dalam POD, kita definisikan koefisien POD $B$, dimana $B_k = \Sigma_k V^T_k$, $B_k \in \mathbb{R}^{k \times m}$. Sehingga persamaannya menjadi:
\[Y \approx U_k B_k\]pod_coeff = sigma_trunc @ vt_trunc
Proper Orthogonal Decomposition (POD) terdiri dari dua komponen besar: komponen matriks basis spasial $U$ dan komponen parameter fisik yang direpresentasikan oleh koefisien POD $B$. Matriks basis spasial $U$, sebagaimana namanya, adalah elemen dasar untuk membentuk solusi penuh dari permasalahan aliran fluida yang kita bahas. Tiap kolom dalam matriks $U$ merepresentasikan masing-masing mode dari solusi penuh sebuah permasalahan. Secara sederhana, mode ini adalah bahan-bahan dasar, dengan menggabungkan mode-mode tersebut dengan proporsi (koefisien) yang sesuai, kira dapat merekonstruksi solusi dari permasalah aliran fluida tersebut. Grafik yang menggambarkan basis orde pertama, orde kedua, dan solusi penuh dari aliran fluida tersedia pada Gambar 6. Pada tahap ini, kita akan menyimpan matriks $U$ untuk digunakan di waktu yang akan datang.
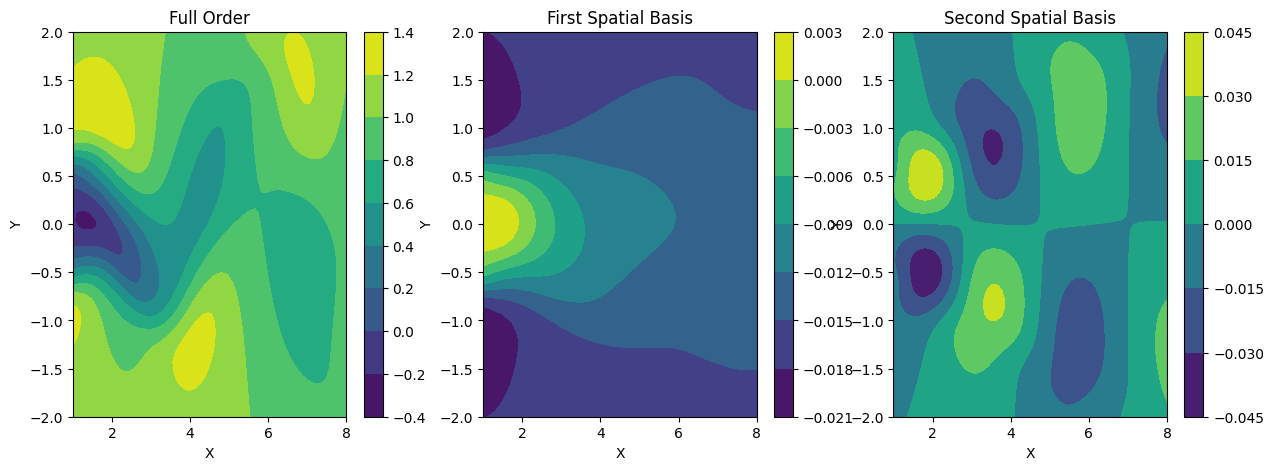
Gambar 6. Basis spasial dari aliran fluida.
Satu kolom di dalam matriks koefisien POD $B$ merepresentasikan “proporsi” dari basis spasial $U$ untuk membentuk sebuah solusi penuh untuk satu parameter, dalam kasus kita, dalam satu waktu. Seperti yang ditunjukkan pada Gambar 7, kolom berwarna merah pada $Y$ merepresentasikan suatu bidang vektor dari sebuah permasalahan untuk satu konfigurasi parameter. Serupa dengan itu, kolom berwarna hijau dalam $B$ merepresentasikan vektor dari koefisien untuk parameter yang sama dengan kolom merah. Dalam kata lain, jika kolom merah merpakan matriks dari aliran fluida pada $t=0$ yang telah diratakan, maka kolom hijau adalah kumpulan dari koefisien yang mengatur matriks basis spasial $U$ pada $t=0$ untuk membentuk kolom merah.
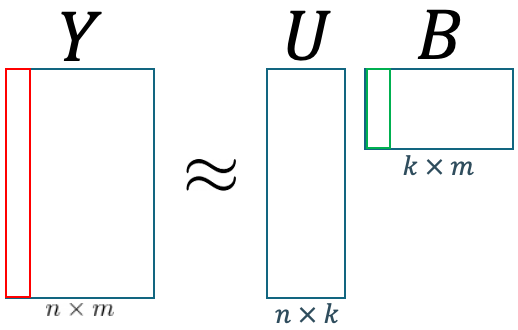
Gambar 7. Ilustrasi POD.
Dengan logika ini, maka jika kita dapat memprediksi nilai koefisien untuk nilai $t$ sembarang, maka kita juga dapat memprediksi perilaku aliran fluida pada $t$ sembarang.
Regression
General Idea
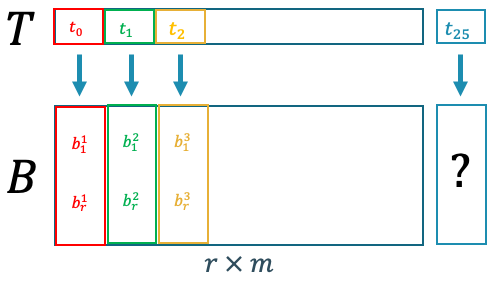
Gambar 8. Pemetaan antara parameter permasalahan $t$ dengan koefisien POD.
Gambar 8 menunjukkan jika kita dapat membuat fungsi yang memetakan antara parameter fisik dan koefisien POD, maka kita dapat memprediksi nilai dari koefisien POD jika diberikan nilai parameter yang tidak diketahui sebelumnya. Karena kita sudah memiliki datanya, kita dapat membuat model regresi yang belajar dari data yang tersedia untuk mengaproksimasi koefisien POD.
\[\hat{b} = f(t)\]Pada dasarnya, kita dapat menggunakan model regresi apapun yang dapat memprediksi nilai kontinu. Namun, perlu diperhatikan bahwa kebanyakan teknik regresi yang tersedia, setidaknya yang tersedia dalam scikit-learn hanya dapat menangani pemetaan one-to-one atau many-to-one. Yang berarti model regresinya dapat menangani permasalahan dengan banyak input dan satu output. Namun, dalam kasus kita, kita memiliki satu input dan banyak output dengan ukuran $k$. Sehingga, dalam kasis kita, kita membutuhkan model regresi sebanyak $k$. Model regresi pertama memprediksi baris pertama dari matriks $B$, model regresi kedua untuk baris kedua, dan seterusnya seperti yang ditunjukkan pada Gambar 9.
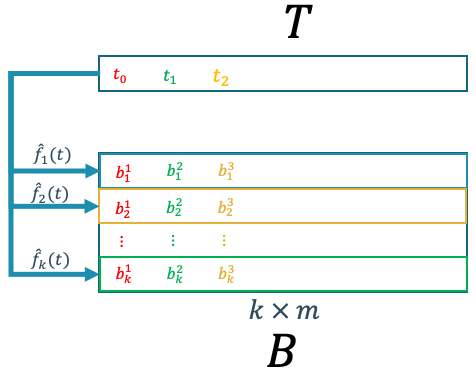
Gambar 9. Skema regresi koefisien POD.
Regresi Polynomial Chaos Expansion (PCE)
Regresi PCE [6] adalah teknik yang populer digunakan dalam bidan kuantifikasi ketidakpastian (UQ), dimana regresi PCE sering digunakan sebagai aproksimasi (surrogate model) dari fungsi evaluasi yang kompleks dan mahal untuk dilakukan seperti eksperimen dan simulasi yang kompleks. Regresi polinomial sederhana secara matematis ditulis sebagai:
\[\hat{f}(X) = \sum_\alpha c_\alpha X^\alpha,\]dimana $\alpha$ adalah derajat dari polinomial, dan $c_\alpha$ adalah koefisien dari polinomial. Sehingga sebagai contoh, jika kita memiliki $\alpha = 2$, maka kita akan mendapatkan persamaan kuadratik $\hat{f}(X) = c_0 + c_1 X + c_2 X^2$.
Regresi PCE memiliki struktur yang mirip dengan regresi polinomial. Namun, alih-alih menggunakan input awal sebagai basis, PCE menggunakan polinomial ortogonal sebagai basis. Beberapa tipe yang sering digunakan adalah polinomial Hermite, polinomial Laguerre, dan polinomial Legendre. Ilustrasi dari polinomial Legendre diberikan dalam Gambar 10. Basis polinomial ortogonal ini ditulis dengan $\phi(X)$.
\[\hat{f}(X) = \sum_{\alpha \in \mathbb{N}^d} c_\alpha \phi_\alpha(X),\] 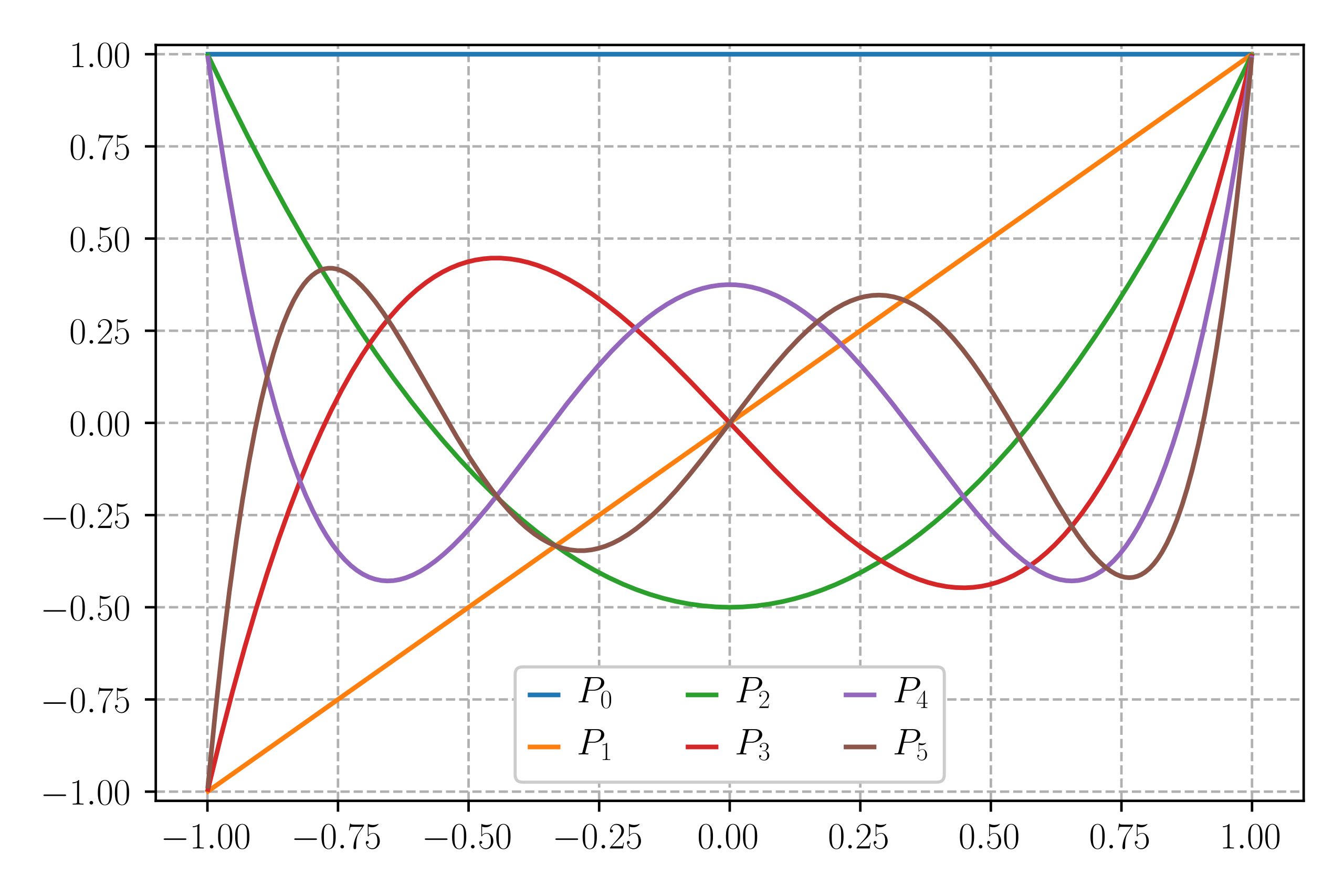
Gambar 10. Ilustrasi 6 polinomial Legendre pertama [7].
Keuntungan dengan menggunakan polinomial ortoginal seperti ini alih-alih menggunakan input original sebagai basis adalah fleksibilitas untuk membentuk relasi kompleks antara parameter fisik dengan koefisien POD.
Untuk menghindari komputasi yang kompleks pada persamaan 6 karena penjumlahan dari seluruh domain, penjumlahan tak terhingga dalam domain tak terhingga tersebut diganti dengan penjumlahan terhingga:
\[\hat{f}(X) \approx \sum_{\boldsymbol{\alpha = 0}}^S c_\alpha \phi_\alpha(\boldsymbol{X}),\]dimana jumlah dari suku ekspansi $S+1$ adalah fungsi dari dimensi $d$ dari $\boldsymbol{X}$ dan orde tertinggi $p$ dari polinomial $\phi(X)$ [8], didefinisikan sebagai:
\[S := \sum_{j=1}^p \frac{1}{j!} \prod_{r=0}^{j-1} (d+r) = \frac{(d+p)!}{d!p!}.\]Walaupun terlihat sedikit mengintimidasi, kita dapat membuat model regresi PCE dengan mudah dengan menggunakan modul Python seperti Chaospy.
Sekarang, kita memiliki pasangan antara parameter fisik dan vektor koefisien POD berjumlah $k$. Dalam kasus ini nilai $k=7$ yang diperoleh dari metode aproksimasi. Mari kita lihat grafik antara waktu $t$ dan dua koefisien POD pertama:
print(f"POD coefficient shape: {pod_coeff.shape}")
print(f"Time vector shape: {t_star.flatten().shape}")
fig1, ax1 = plt.subplots(1, 2, figsize=(14, 5))
# Plot full-order solution
ax1[0].scatter(t_star.flatten(), pod_coeff[0,:])
ax1[0].set_xlabel('t')
ax1[0].set_ylabel('1st POD coeff')
# Plot first basis function
ax1[1].scatter(t_star.flatten(), pod_coeff[1,:])
ax1[1].set_xlabel('t')
ax1[1].set_ylabel('2nd POD coeff')
plt.show()

Gambar 11. Grafik antara waktu dan nilai dua koefisien POD pertama.
Jelas terlihat bahwa hubungan antara waktu dan dua koefisien POD pertama memiliki hubungan peridoing, dan kemungkinan juga pada koefisien lainnya. Penting untuk dicatat bahwa versi dasar dari PCE mungkin tidak akan secara efektif memodelkan hubungan periodik, sehingga anda mungkin akan memerlukan model yang lebih cocok. Namun demikian, untuk tujuan tutorial dasar dan singkat, saya akan melanjutkan dengan versi dasar PCE sebagai demonstrasi. Kode PCE dibawah ditulis dengan menggunakan modul chaospy. Namun, saya tidak akan membahas per baris, penjelasan yang lebih mendetil mengenai chaospy dapat ditemukan dalam dokumentasi resmi.
import chaospy
from sklearn.linear_model import LinearRegression
def train_pce(x, pod_coeff):
# Train multiple PCE models
1 = chaospy.Uniform(0,1)
expansion = chaospy.generate_expansion(15, x1)
model = LinearRegression(fit_intercept=False)
#normalize time with 20 (max t in dataset)
norm_x = x/20
pce_list = []
for i in range(pod_coeff.shape[0]):
surrogate,coefs = chaospy.fit_regression(expansion, norm_x, pod_coeff[i,:].reshape(-1,1),
model=model, retall=True)
pce_list.append(surrogate)
return pce_list
Kita hanya akan menggunakan data dari waktu $0$s sapai $7.5$s untuk melatih modelnya.
t_train = t_star.flatten()[:75]
coeff_train = pod_coeff[:,:75]
pce_list = train_pce(t_train, coeff_train)
Sekarang, kita akan prediksi koefisien POD dari waktu 0-8s.
first_coeffs = pce_list[0](np.linspace(0,8,500)/20)
second_coeffs = pce_list[1](np.linspace(0,8,500)/20)
fig1, ax1 = plt.subplots(1, 2, figsize=(14, 5))
# Plot full-order solution
ax1[0].scatter(t_train, coeff_train[0,:], label="training data")
ax1[0].plot(np.linspace(0,8,500), first_coeffs.flatten(), 'orange', label="predicted")
ax1[0].set_xlabel('t')
ax1[0].set_ylabel('1st POD coeff')
ax1[0].legend()
# Plot first basis function
ax1[1].scatter(t_train, coeff_train[1,:], label="training data")
ax1[1].plot(np.linspace(0,8,500), second_coeffs.flatten(), 'orange', label="predicted")
ax1[1].set_xlabel('t')
ax1[1].set_ylabel('2nd POD coeff')
ax1[1].legend()
plt.show()
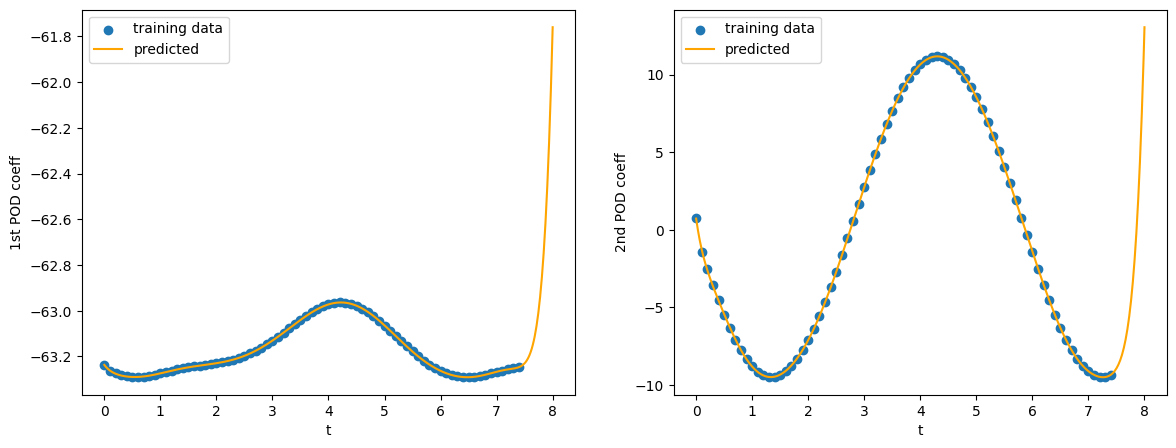
Gambar 12. Grafik antara waktu dan nilai dua koefisien POD pertama yang diprediksi.
Hasil prediksi dari dua koefisien POD pertama menunjukkan bahwa PCE tidak bisa menangkap komponen periodik dari data koefisien POD, bahkan ketika model menunjukkan hasil yang baik dalam data latih. Sehinnga, perlu digunakan model yang lebih cocok. Namun, tugas ini saya serahkan kepada pembaca sebagai latihan.
Dengan mengasumsikan bahwa kita memiliki model yang tepat untuk memprediksi perilaku koefisien POD, kita dapat memprediksi solusi dari aliran fluida. Dengan sebelumnya kita telah memiliki koefisien POD yang telah diprediksi, solusi dari aliran fluida dapat dihitung dengan:
\[Y \approx U_k B_k\]In our case, let’s try to predict the flow field at $t=7.7 s$
def predict_all_coeff(x, pce_list):
pred_coeffs = []
x_norm = x/20 # normalize input with 20 (max t in dataset)
for pce in pce_list:
temp = pce(x_norm)
pred_coeffs.append(temp)
pred_coeffs = np.concatenate(pred_coeffs, axis=0)
return pred_coeffs
pred_coeffs = predict_all_coeff(7.7, pce_list)
predicted_field = u_trunc @ pred_coeffs.reshape(-1,1)
# Try plotting first basis function of POD
ref = snapshot[:,77].reshape(50,100) # get first order basis
predicted = predicted_field[:,0].reshape(50,100) # get first order basis
fig1, ax1 = plt.subplots(1, 2, figsize=(14, 5))
# Plot full-order solution
cf = ax1[0].contourf(x_grid,y_grid,ref)
cbar = fig1.colorbar(cf, ax=ax1[0])
ax1[0].set_xlabel('X')
ax1[0].set_ylabel('Y')
ax1[0].set_title('Original field at t=7.7')
# Plot first basis function
cf1 = ax1[1].contourf(x_grid,y_grid,predicted)
cbar1 = fig1.colorbar(cf1, ax=ax1[1])
ax1[1].set_xlabel('X')
ax1[1].set_ylabel('Y')
ax1[1].set_title('Predicted field at t=7.7')
plt.show()

Gambar 13. Prediksi aliran fluida pada t=7.7 s.
Akhirnya, kita dapat menyimpulkan bahwa teknik proper orthogonal decomposition (POD) memberikan metode yang efektif untuk mengurangi dimensi/kompleksitas dari permasalahan bidang vektor. Namun, agar dapat memprediksi perilaku sistem dengan akurat, model prediksi yang sesuai perlu untuk dipilih dengan benar. Meskipun demikian, artikel tutorial ini memberikan gambaran dan ide umum untuk bagaimana melakukan prediksi pada permasalahan bidang vektor yang kompleks, seperti aliran fluida, dengan cara mereduksi dimensi dengan menggunakan proper orthogonal decomposition.
Sitasi artikel ini:
@misc{faza2024basicpodpce,
author = {Faza, Ghifari Adam},
title = {Simple Vector Field Prediction using Proper Orthogonal Decomposition and Polynomial Chaos Expansion (POD-PCE)},
month = {April},
year = {2024},
url = {https://fazaghifari.github.io/posts/2024/04/pod-pce-basic-en/},
}
References
- M. Loéve, Fonctions Al ́eatoires de Second Ordre (Random Functions of Second Order), Gauthier-Villars, 1970.
- G. Berkooz, P. Holmes, J. L. Lumley, The proper orthogonal decomposition in the analysis of turbulent flows, Annual Review of Fluid Mechanics 25 (1993) 539–575. URL: https://doi.org/10.1146/annurev.fl.25.010193.002543. doi:10.1146/annurev.fl.25.010193.002543.
- J. Cusumano, M. Sharkady, B. Kimble, Spatial coherence measurements of a chaotic flexible-beam impact oscillator (1993) aerospace structures: Nonlinear dynamics and system response, American Society of Mechanical Engineers, AD-33 (1993) 13–22.
- A. Chatterjee, An introduction to the proper orthogonal decomposition, Current Science 78 (2000) 808–817. URL: http://www.jstor.org/stable/24103957.
- https://en.wikipedia.org/wiki/Singular_value_decomposition#
- R. Ghanem, P. D. Spanos, Polynomial chaos in stochastic finite elements, Journal of Applied Mechanics 57 (1990) 197–202. URL:https://doi.org/10.1115/1.2888303. doi:10.1115/1.2888303.
- https://en.wikipedia.org/wiki/Legendre_polynomials
- D. Xiu, G. E. Karniadakis, The wiener–askey polynomial chaos for stochastic differential equations, SIAM Journal on Scientific Computing 24 (2002) 619–644.URL: https://doi.org/10.1137/s1064827501387826.doi:10.1137/s1064827501387826
